本教程包含以下部分：

① 玻璃光纤中的导光

② 光纤模式

③ 单模光纤

④ 多模光纤

⑤ 光纤末端

⑥ 光纤接头

⑦ 传播损耗

⑧ 光纤耦合器和分路器

⑨ 偏振问题

⑩ 光纤的色散

⑪ 光纤的非线性

⑫ 光纤中的超短脉冲和信号

⑬ 附件和工具

这是 Paschotta 博士的无源光纤教程的第 2 部分

第二部分：光纤模式

通常，在光纤中传播的光的强度分布在传播过程中会发生变化。它甚至经常以相当复杂的方式发展。例如，看看如果我们将高斯光束（相对于光束轴倾斜 20°）注入纤芯半径为 20 μm 且 NA 为 0.3 的光纤会发生什么情况：

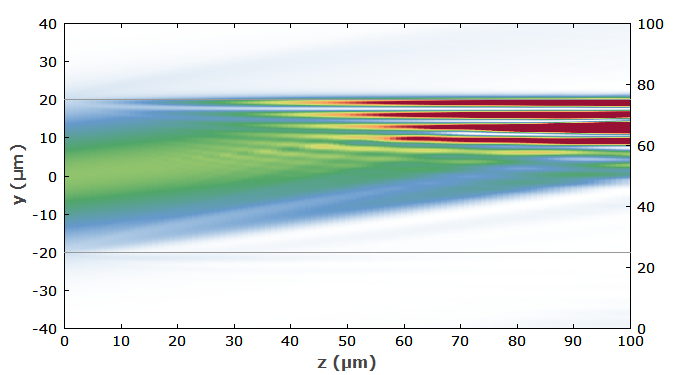图 1： 使用 RP Fiber Power 软件 模拟的多模光纤中强度的演变。将与光束轴成 20° 角的高斯光束注入光纤。

（请注意，这里我们只显示强度分布，因为显示的空间区域较大，因此很难显示波前。）

可以清楚地看到当光束到达纤芯/包层界面并在那里反射时发生的干涉效应。最后，横向光束轮廓如图 2 所示：

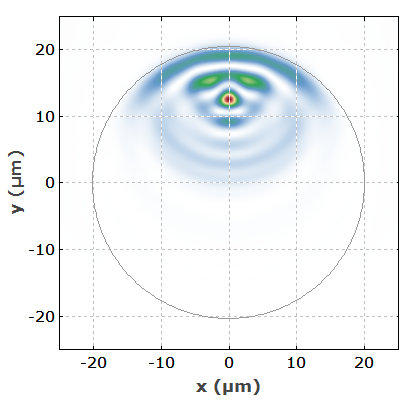图 2：传播超过 100 μm 后光纤中的光束轮廓。

我们已经看到强度分布通常以复杂的方式演变。然而，存在某些幅度分布（即电场幅度的分布），其中强度分布在传播期间保持不变（假设是无损光纤）。这种场分布称为光纤的模式。其中最简单的基本模式，也称为 LP 01模式，对于当前示例中的光纤如下所示：

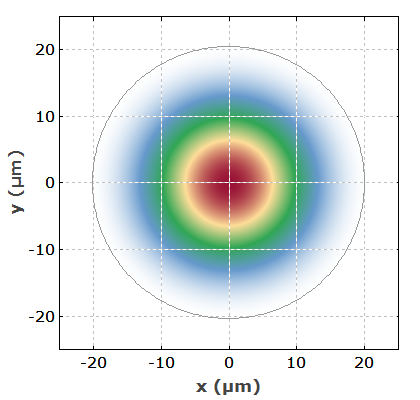图 3：模光纤中基模的强度分布。灰色圆圈表示纤芯/包层边界。

这是一个高阶模态，LP 37模态：

图4：多模光纤中 LP 37模式的 强度分布。

至于基本模式，自然背离正好被不均匀的指数分布所抵消。请注意，特别是高阶模式可以具有显着延伸到包层中的轮廓。下图显示了光纤所有导模的振幅分布，按其模式指数排序：

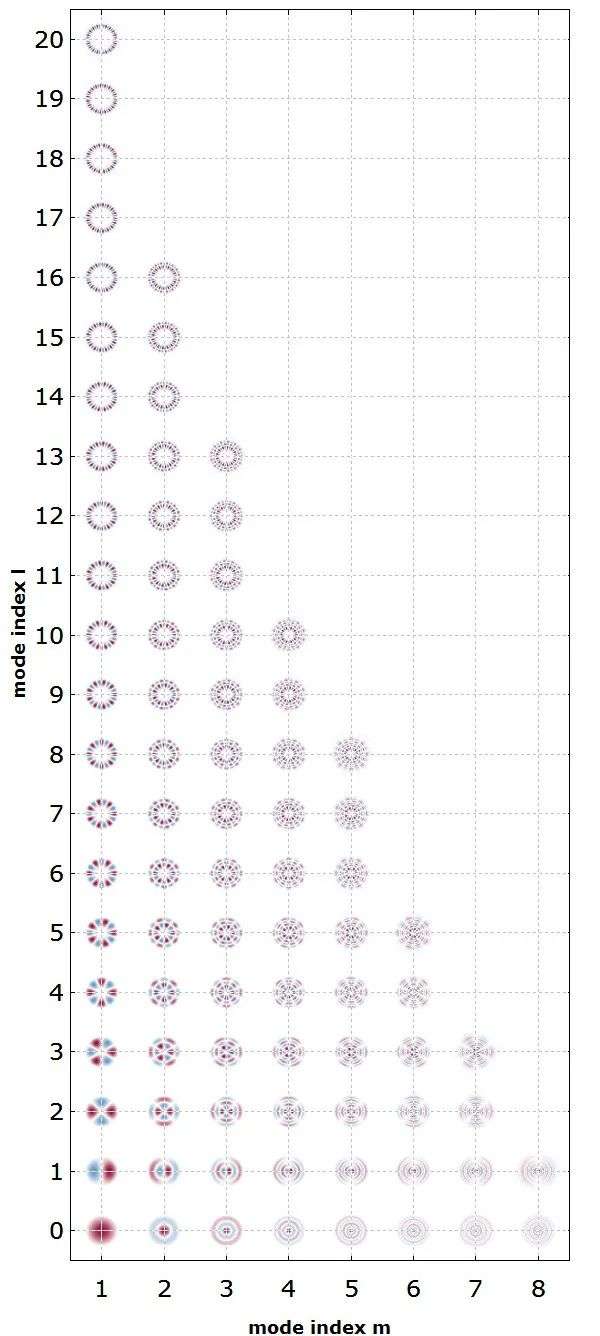图 5：多模光纤的所有导模的幅度分布。RP Fiber Power 软件 已在远低于一秒的时间内计算出这些模式。

在我们的示例中，纤芯半径为 20 μm，NA = 0.3，光纤在 1.5 μm 波长处有 84 个不同的导模（见图 5）——当计算模式的不同方向时，甚至有 160 个。（例如，LP11模式也存在于旋转 90° 的版本中；这两个模式是相互正交的。）所有的导模基本上都限制在纤芯区域，即使它们可以在一定程度上延伸到包层中（但随着距离的增加强度会降低从核心）。

图 6 显示了光纤模式的远场分布，因为它们可以在离光纤末端很远的地方观察到。它们看起来与近场剖面相似，但不仅仅是它们的重新缩放版本。（您不能指望为特定光纤结构计算的模式同时是自由空间的模式！）另外请注意，例如，虽然所有 LP0m 模式都大约填充了整个光纤纤芯并因此具有相似的尺寸，但发散度（在远场中看到）随着 m 的增加而变得更大。

图 6： 与图 5 相同的光纤的远场剖面。

还有许多非引导模式，称为包层模式，可以延伸到整个包层（和核心）。由于包层通常比纤芯大得多，并且通常具有更高的数值孔径（由于与其周围的涂层具有较大的折射率对比），因此包层通常比纤芯具有更多的模式。

如果折射率分布具有圆柱对称性，我们将获得所谓的 LP 模式。这些数值计算相对容易，即使对于折射率的任意径向相关性，也不仅适用于阶跃折射率光纤。例如，RP Fiber Power 软件可以在几分之一秒内计算出我们的阶跃折射率光纤的所有模式，并且对于例如超高斯径向轮廓同样快。对于非径向对称的折射率剖面，需要更复杂的数值方法来计算所有模式，这需要更多的计算时间。

模式的基本事实

我们现在看看模式的各种有趣的属性：

• 如前所述，模式的强度分布在光纤中传播期间保持恒定（参见图 6），至少如果它是无损的。复振幅分布确实发生了变化，但只是以一种简单的方式：复相位与传播长度成比例地发展：φ  =  β z 与相位常数 β。请注意，此相变同样适用于轮廓的所有横向位置。每个模式都有自己的 β 值，尽管可能会出现模式退化（不同模式的相同 β 值）。

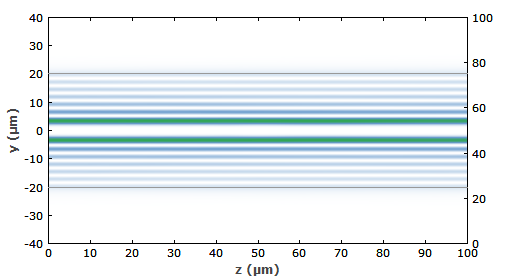图 7：LP 37模式 的光束轮廓演变。强度分布保持不变。

• 对于无损光纤，模式的相位前总是平面的。坡印廷矢量，显示能量流的方向，在整个模式分布中始终平行于光纤轴。
• 如果存在传播损耗，例如由于光纤纤芯中的掺杂剂，模式会有所改变。波前现在可能会弯曲，表明径向方向的能量流。（例如，如果我们只在纤芯吸收，能量必须从包层流向纤芯。但在大多数情况下，波前只有边缘变形。）然后光功率沿传播方向呈指数下降；传播常数得到一个实部，减去幅度吸收系数。
• 通常，导模的数量随着波长变短而增加。对于长波长，可能只有一个导模（→ 单模光纤），或者实际上根本没有导模。（阶跃折射率分布总是至少具有基模，但对于某些光子晶体光纤，情况并非如此。）
• 对于任何导光，这些模式形成了基础（在数学意义上），即完整的正交系统。换句话说，任何由光纤引导的复振幅分布都可以表示为模式的线性叠加。这种模式分解可以对单色光进行，也可以对多色光进行；在后一种情况下，只需分别对每个频率分量进行分解。
  

模式的重要属性

请注意，不同模式的叠加通常不是模式本身。一般来说，不同的模式有不同的 β 值。因此，它们的相位演变是不同的，并且在传播过程中，由于干扰条件的变化，整体强度分布也会发生变化。如果我们只有两个模式被激发，我们会得到一个简单的模式跳动，其中强度分布的形状周期性地变化；周期与 β 值的差异成反比。周期与如果激发了许多具有不同 β 值的模式，则演化变得非常复杂。对于给定的波长，每种光纤模式都有几个重要的特性：

• 它具有一定的复振幅分布，从中可以获得强度分布。
• 根据强度分布，可以计算出有效模式面积。这决定了非线性效应的强度。
• 相位常数 β 说明了其在传播过程中的整体复杂相位变化的速度。对于强导模，它远高于包层的相位常数。在那种情况下，强度分布基本上不会延伸到包层中。
• 从 β 关于光频率的一阶和二阶导数，可以计算群速度和群速度色散(GVD)。
• 对于有损光纤，每个模式都可以有一定的衰减常数。这些值在模式之间可能会有很大差异——有时相差几个数量级。例如，对于高阶模式，弯曲损耗通常要高得多。它们可以用数值光束传播来计算，也可以用一些分析技术来估计。顺便说一句，弯曲也可以改变和扭曲模式分布。
• 截止波长是模式不再存在的波长。（在某些情况下，模式可以有更高和更低的截止值。）

降低高阶模式的相位延迟

高阶模式比低阶模式具有更大的横波矢量分量。由于具有这种波矢量的平面波分量相对于光纤轴倾斜，因此可以预期它具有增加的路径长度，因此高阶模式将经历比例如基模更大的相位延迟。然而，事实恰恰相反！较大的横向波矢量分量意味着较小的纵向分量，这意味着减小的相位延迟。所以实际上最高阶模式的相位常数（ β 值）是最低的，并且通常接近于包层的折射率乘以真空波数。

顺便说一下，这种模式在包层中也表现出缓慢的强度衰减，即它们的强度分布延伸到包层中很远。这些模式的另一个特性是降低的群速度（参见关于色散的第 10 部分）。这实际上适合增加的路径长度，但上面解释的可能令人惊讶的发现应该是一个警告：小心对那种模糊类型的快速“解释”。

基于模式计算光的传播

使用计算的一组模式，可以计算在光纤中传播任意距离后任意输入轮廓的结果场轮廓：

• 首先，通过输入幅度分布与所有模式幅度分布的复共轭的复重叠积分来计算所有导模的激励幅度。
• 然后根据它们的 β 值改变所有模式的复振幅。
• 通过将模式的所有贡献相加来构建最终的光束轮廓。
  

请注意，此过程在计算上并不困难，除非在折射率分布不是径向对称的情况下，光纤具有大量模式和/或复杂模式。计算量不依赖于传播距离。（对于数值光束传播，更长的距离通常需要更多的时间。）

在某些情况下，模式耦合计算是有帮助的。例如，可以计算“未受干扰”光纤的模式，然后计算由一些附加效应引起的模式耦合。例如，光纤布拉格光栅中的周期性折射率调制可以耦合反向传播或同向传播模式。

模式方法的局限性

模式的概念通常非常方便进行计算，如上所示。但是，它也有其局限性：

• 在某些情况下——例如，对于任意索引配置文件——模式很难计算。
• 在有大量模式的情况下，基于它们进行计算也可能不方便。注意：如果需要考虑包层模式，即使核心只有很少的导模，在计算中也会出现大量模式。
• 弯曲等额外的干扰已经使模式的计算变得更加困难。
• 如果模态特性沿光纤长度发生变化（例如，对于锥形光纤），该概念至少也更难应用。

由于这些原因，通常需要直接数值光束传播而不是模式概念。

下一期将介绍第三部分：单模光纤

敬请关注！