水下LED诱鱼灯设计与分析及其光传播（二）

作者：Sheng Chih Shen，Cheng Yuan Kuo1，Ming-Chung Fang

台湾台南国立成功大学系统与海军机电工程系

审校：许东

译注：本文系统的介绍了水下LED光源的水下传输模型的建立，用于LED集鱼灯的设计参考，是一篇具有深度研究价值的参考论文。

本文内容较长，分三部分发布。

（前一部分）

散射角α的粒子散射后，平均余弦如下：

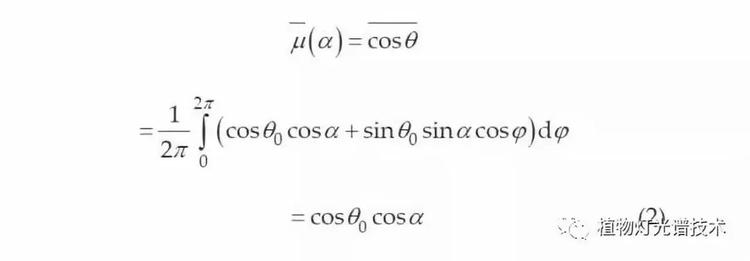
一旦计算出散射角α的平均余弦，就将0→π的角度分成相等大小的N个段，并且在下面获得随机数α的平均余弦：

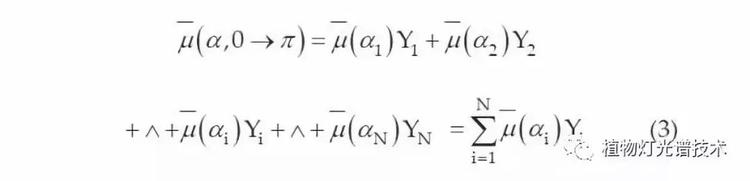
其中αi是观察到的第i个角度段的中点，Yi是散射后粒子落在第i个角度段上的概率。

基于相位散射函数，Yi定义为：

Yi=2πβ(αi)sinαiΔα （4）

其中β（αi）是相位散射函数。

从式（2），（3）和（4），得到下式：

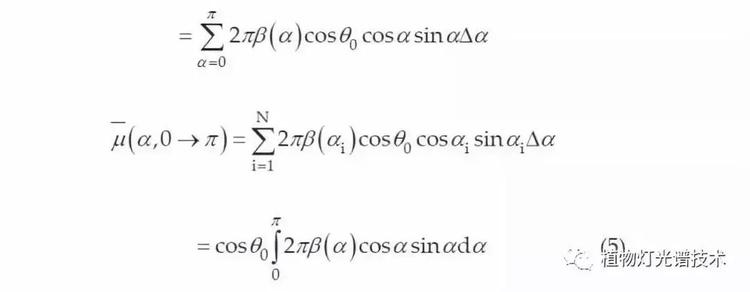
上式的积分定义了的平均余弦基于：

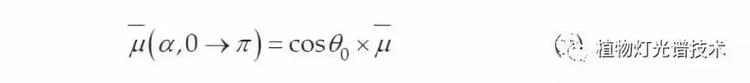
公式（6）表示在发射角θ0的光束入射到水面上并经历一次散射事件之后平均余弦的变化。

因此，假设入射光的平均余弦为μ0，则光束经过n次散射后的最终平均余弦为：

显然，随着水下行进的光束一次又一次地散射，其平均余弦将不断减小。

此外，平均余弦的衰减率取决于散射相位函数β（θ）。

光束在行进散射多次后几乎会扩散。因此，平均余弦越小，光束散射的次数越多，光束越近扩散状态。

另外，可以计算在水下行进的光束的散射概率。

假设光在水下行进一段距离L，其散射概率由P（0），P（1），P（2），.... P（n）给出。

P（0）表示无散射，P（1）表示一个散射事件，P（2）表示两个散射事件；以此类推。

其中，P（0）意味着没有散射，且定义为：

P(0)=exp(bL)（8）

其中b是散射系数。

P（1），即光束在整个路径L上，行进后仅发生一次散射事件的概率，定义为：

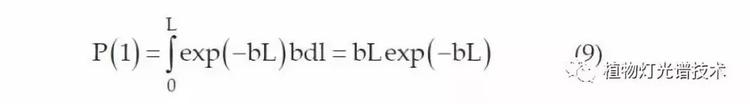
因此，P（n），即光束在整个距离L后传播的n个散射事件的概率，可以定义为：

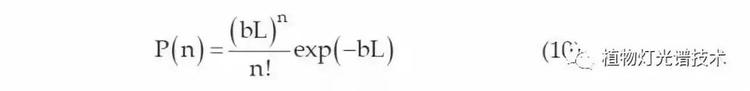
图3（a）和3（b）显示了在不同水体中行进20米的光束所经历的散射事件。 根据Kirk（1999）。

散射系数：

b = 0.059表示略微混浊的水质

b = 0.321表示轻度混浊的水体

b = 1.719表示高度混浊的水体。

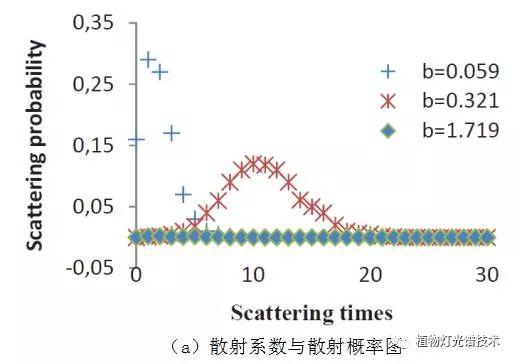
（译注：Scattering times散射次数，Scattering probability散射概率）

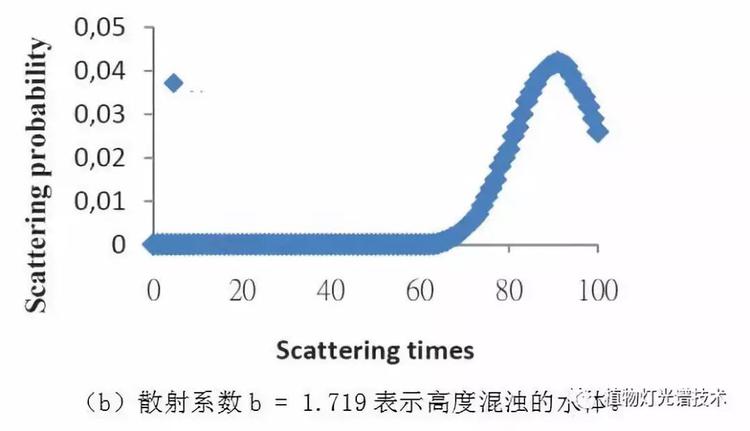
图3.不同水质中行进20米处光束的散射概率与散射时间之间的关系。

图3（a）显示在不同的水质中，行进相同距离的光束经历大量不同的散射事件。对于在略微混浊的水中行进20m的光束，16％的光子不散射，但29％和27％分别经历1和2次散射事件。

换句话说，超过70％的光束在整个转移过程中经历不超过两次散射事件，其余的散射不超过4或5次。

在适当浑浊的水中，大多数光束散射5到15次。

然而，在高度混浊的水中，结果完全不同。如图3（b）所示，高度混浊水中的最大散射量约为90次。

此外，如图4所示，平均余弦随散射次数而变化。也就是说，散射过程对平均余弦有显着影响，尤其是前15个事件。准直光束散射5次后，其平均余弦下降到0.6，然后在15次散射事件后下降到0.3以下。

一旦散射事件的数量超过50，平均余弦近0，表光束是漫射的。即当光束在浑浊的水体中行进超过20米时，几乎所有的光能都已经散开。因此，水下光散射的分析揭示了光束如何被转移以及其发光强度如何衰减。

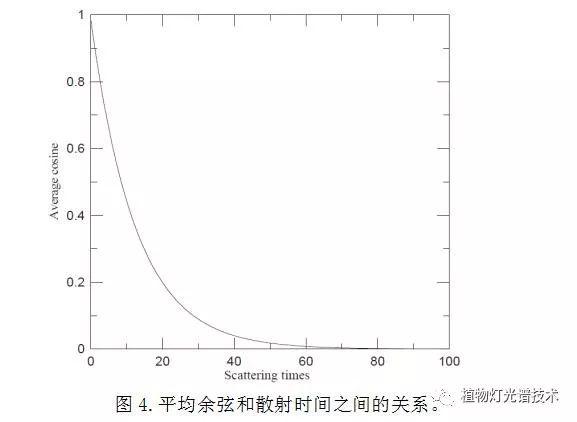
（译注：Average cosine平均余弦）

公式（7）定义了光束在经历n次散射事件之后的平均余弦。

公式（10）定义了光束在行进有限距离L并经历n次散射事件之后的散射概率， 水下光束的平均余弦μ（L）可以在行进距离L后得到：

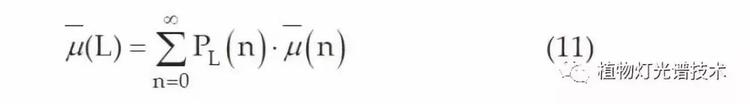
当衰减系数导入散射因子后，衰减函数将随行程距离L，散射次数n和吸收系数a而变化，定义如下：

其中a是光束的吸收系数，C（L）是任意随机行程距离L的衰减函数。

最后，具有散射函数的水下光束的传递公式由下式给出：

IL=I0exp（C(L)×L）（13）

其中IL是行进距离L处的发光强度

I0是光源强度，C（L）是总衰减系数。

2.2 LED光源特性

作为LED光源最重要的特性，（LIDC）包括发射角与轴向光强度分布之间的关系。 从传统的光源或点光源来看，传统光源是朗柏型配光; 因此，它的发光强度在不同的角度是相同的。

相比之下，LED光源是定向的和扇形的; 因此，其发光强度随发射角度的不同而变化。对于朗伯型光源，每个发射角度及其发光强度通常可以通过公式（14）表示。配光的有效发射角被定义为具有轴向发光强度的50％的对应角度。

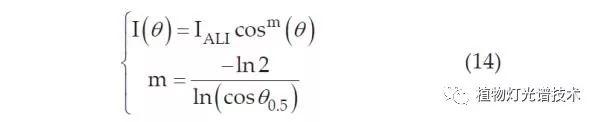
在不同LED 的（LIDC）形状下，公式（14）可用于计算轴向发光强度的（IALI）。通过对水下光传输模型公式（13）与公式（14），即对散射函数进行积分，可以获得水下任意点的LED光源的度E；因此，选择合适的LIDC以匹配水的浊度对于光模块设计至关重要。

E(θ,l)=I(θ)cosθ×exp（15）

公式（15）是结合（13）和（14）的公式，是基于LED光源的特性。

本研究综合了光场的平均余弦和光散射概率的方法与关于在水下传输的定向光束模型，本研究分析了其在不同距离处的散射情况以及其光场角分布的变化；基于这个数学模型，作者构建了水下LED光源的传递模型。

（未完待续....）